The tension in the rope is constant and equal to 40 N as the block is pulled. What is the instantaneous power (in W) supplied by the tension

Question

The tension in the rope is constant and equal to 40 N as the block is pulled. What is the instantaneous power (in W) supplied by the tension in the rope if the block when the block is 5 m away from its starting point? The coefficient of kinetic friction between the block and the floor is 0.2 and you may assume that the block starting at rest.

in progress 0
Ngọc Khuê 4 years 2021-08-04T22:47:33+00:00 1 Answers 14 views 0

Answers ( )

  1. lethu
    0
    2021-08-04T22:49:02+00:00
    Reply

    Complete Question:

    A 10 kg block is pulled across a horizontal surface by a rope that is oriented at 60° relative to the horizontal surface.

    The tension in the rope is constant and equal to 40 N as the block is pulled. What is the instantaneous power (in W) supplied by the tension in the rope if the block when the block is 5 m away from its starting point? The coefficient of kinetic friction between the block and the floor is 0.2 and you may assume that the block starting at rest.

    Answer:

    Power = 54.07 W

    Explanation:

    Mass of the block = 10 kg

    Angle made with the horizontal, θ = 60°

    Distance covered, d = 5 m

    Tension in the rope, T = 40 N

    Coefficient of kinetic friction,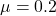 \mu = 0.2

    Let the Normal reaction = N

    The weight of the block acting downwards = mg

    The vertical resolution of the 40 N force, f_{y} = 40sin \theta

    \sum f(y) = 0

    N + 40 sin \theta - mg = 0\\N = -40sin60 + 10*9.81 = 0\\N = 63.46 N

    \sum f(x) = 0

    40 cos 60 - f_{r} - ma = 0\\ f_{r} = \mu N\\ f_{r} = 0.2 * 63.46\\ f_{r} = 12.69 N\\40cos 60 - 12.69-10a = 0\\7.31 = 10a\\a = 0.731 m/s^{2}

    v^{2} = u^{2} + 2as\\u = 0 m/s\\v^{2} = 2 * 0.731 * 5\\v^{2} = 7.31\\v = \sqrt{7.31} \\v = 2.704 m/s

    Power, P = Fvcos \theta

    P = 40 *2.704 cos60\\P = 54.074 W

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )