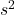The student in item 1 moves the box up a ramp inclined at 12 degrees with the horizontal. If the box starts from rest at the bottom of the r

Question

The student in item 1 moves the box up a ramp inclined at 12 degrees with the horizontal. If the box starts from rest at the bottom of the ramp and is pulled at an angle of 25 degrees with respect to the incline and with the same 185 N force, what is the acceleration up the the ramp? Assume that the coefficient of kinetic friction is 0.27

in progress 0
Neala 4 years 2021-08-12T17:12:33+00:00 1 Answers 24 views 0

Answers ( )

  1. yenoanh
    0
    2021-08-12T17:13:34+00:00
    Reply

    Answer:

    Acceleration up the ramp =  -2.745 m/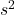s^{2}

    Explanation:

    Given

    box is pulled at angle Θ =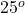 25^{o}

    Force applied F = 185N

    coefficient of friction, μ_{k} = 0.27

    mass of the box m = 35 kg

    We know that,

    acceleration due to gravity g = 9.8 m/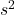s^{2}

    horizontal component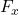 F_{x} = F cosΘ = 185 * cos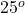25^{o} =167.67

    vertical component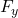 F_{y} = F sinΘ =185*sin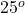25^{o} = 78.18

    Another vertical component is due to gravity F_{g} , force in given by

    F_{g} = mg

        = 35 x 9.8

        = 343.35 N

    Normal force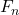 F_{n} = F_{g}  – F_{y}

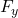
                                = 343.35 – 78.18

                                = 265.17 N

    Frictional force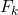 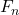F_{k} = F_{n} * μ_{k}

                                   = 265.17 * 0.27

                                   = 71.596 N

    To find acceleration, we know that,

    force = mass x acceleration

    acceleration =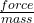 \frac{force}{mass}

    Here force is the summation of frictional force and horizontal component of the applied force. These force act in opposite directions.

    force =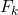  F_{k} – F_{x}

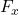
             = 71.596 – 167.67

             = -96.074

    acceleration =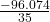 \frac{-96.074}{35}

                         = -2.745 m/s^{2}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )