The recursive function LaTeX: f\left(0\right)=1,\:f\left(n\right)=f\left(n-1\right)+2nf ( 0 ) = 1 , f ( n ) = f ( n − 1 ) + 2 n represents

Question

The recursive function LaTeX: f\left(0\right)=1,\:f\left(n\right)=f\left(n-1\right)+2nf ( 0 ) = 1 , f ( n ) = f ( n − 1 ) + 2 n represents

in progress 0
Adela 4 years 2021-08-29T00:35:09+00:00 1 Answers 10 views 0

Answers ( )

  1. thanhha
    0
    2021-08-29T00:36:14+00:00
    Reply

    Question:

    The recursive function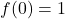 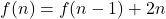f(0) = 1, f(n) = f(n-1) + 2n represents the nth term of a sequence. Determine the explicit function

    Answer:

    f(n) = n^2 + n+1

    Step-by-step explanation:

    Given

    f(0) = 1

    f(n) = f(n-1) + 2n

    Required

    Write an explicit formula

    Let n = 1

    f(1) = f(1-1) + 2*1

    f(1) = f(0) + 2

    f(1) = 1 + 2 = 3

    Let n = 2

    f(2) = f(2-1) + 2*2

    f(2) = f(1) + 4

    f(2) = 3 + 4 = 7

    Let n =3

    f(3)=f(3-1) + 2 * 3

    f(3)=f(2) + 6

    f(3)=7+ 6 = 13

    Let n = 4

    f(4) = f(4 - 1) + 2 * 4

    f(4) = f(3) + 8

    f(4) = 13+ 8 = 21

    So, we have:

    f(1) = 3= 1 + 2 * 1=1+0*1*2*1

    f(2) = 7= 3 + 2 * 2=1+1*2+2*2  

    f(3) = 13= 7 + 2 * 3= 1+2*3+2*3

    f(4) = 21 = 13 + 2 * 4= 1+3*4 +2 *4

    Following the above pattern:

    f(n) = 1 + (n - 1) * n + 2 * n

    f(n) = 1 + n(n - 1) + 2n

    Open bracket

    f(n) = 1 + n^2 - n + 2n

    f(n) = 1 + n^2 + n

    f(n) = n^2 + n+1

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )