The length of a rectangle is 2 feet less than 4 times the width. The area is 256ft2. Find the dimensions of the rectangle.

Question

The length of a rectangle is 2 feet less than 4 times the width. The area is 256ft2. Find the dimensions of the rectangle.

in progress 0
Thành Đạt 4 years 2021-08-24T03:35:32+00:00 1 Answers 9 views 0

Answers ( )

  1. linhdan
    0
    2021-08-24T03:37:21+00:00
    Reply

    Answer:

    W = 8.255

    L = 31.02

    Step-by-step explanation:

    Let L = Length and W = Width.

    So:

    L = 4W - 2

    Area = 256

    Required

    Find L and W

    Area is calculated as:

    Area = L * W

    Substitute 4W – 2 for L and 256 for Area

    Area = (4W - 2) * W

    256 = (4W - 2) * W

    Open Bracket

    256 = 4W^2 - 2W

    Divide through by 2

    128 = 2W^2 - W

    Equate to 0

    2W^2 - W - 128 = 0

    An equation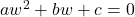 aw^2 + bw + c = 0 has the roots

    W = \frac{-b\±\sqrt{b^2 - 4ac}}{2a}

    Where

    a = 2   b = -1 c = -128

    So:

    W = \frac{-(-1)\±\sqrt{(-1)^2 - 4*2*-128}}{2*2}

    W = \frac{1\±\sqrt{1 +1024}}{4}

    W = \frac{1\±\sqrt{1025}}{4}

    W = \frac{1\± 32.02}{4}

    W = \frac{1+ 32.02}{4} or W = \frac{1 - 32.02}{4}

    W = \frac{33.02}{4} or W = \frac{-31.02}{4}

    W = 8.255  or W = -7.755

    But the dimension can not be negative.

    So:

    W = 8.255

    Recall:

    L = 4W - 2

    L = 4 * 8.255 - 2

    L = 31.02

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )