The image of a parabolic lens is projected onto a graph. The image crosses the x-axis at –2 and 3. The point (–1, 2) is also on the parabola

Question

The image of a parabolic lens is projected onto a graph. The image crosses the x-axis at –2 and 3. The point (–1, 2) is also on the parabola. Which equation can be used to model the image of the lens?

y = (x – 2)(x + 3)
y = (x – 2)(x + 3)
y = (x + 2)(x – 3)
y = (x + 2)(x – 3)

in progress 0
Khoii Minh 4 years 2021-09-05T08:55:18+00:00 1 Answers 222 views 0

Answers ( )

  1. Helga
    0
    2021-09-05T08:56:20+00:00
    Reply

    Given:

    The image of a lens crosses the x-axis at –2 and 3.

    The point (–1, 2) is also on the parabola.

    To find:

    The equation that can be used to model the image of the lens.

    Solution:

    If the graph of polynomial intersect the x-axis at c, then (x-c) is a factor of the polynomial.

    It is given that the image of a lens crosses the x-axis at –2 and 3. It means (x+2) and (x-3) are factors of the function.

    So, the equation of the parabola is:

    y=k(x+2)(x-3)          …(i)

    Where, k is a constant.

    It is given that the point (–1, 2) is also on the parabola. It means the equation of the parabola must be satisfy by the point (-1,2).

    Putting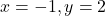 x=-1, y=2 in (i), we get

    2=k(-1+2)(-1-3)

    2=k(1)(-4)

    2=-4k

    Divide both sides by -4.

    \dfrac{2}{-4}=k

    -\dfrac{1}{2}=k

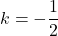    Putting k=-\dfrac{1}{2} in (i), we get

    y=-\dfrac{1}{2}(x+2)(x-3)

    Therefore, the required equation of the parabola is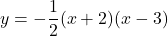 y=-\dfrac{1}{2}(x+2)(x-3).

    Note: All options are incorrect.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )