Tendons are, essentially, elastic cords stretched between two fixed ends; as such, they can support standing waves. These resonances can be

Question

Tendons are, essentially, elastic cords stretched between two fixed ends; as such, they can support standing waves. These resonances can be undesirable. The Achilles tendon connects the heel with a muscle in the calf. A woman has a 20–long tendon with a cross-section area of 130 . The density of tendon tissue is 1100 .
For a reasonable tension of 600 , what will be the fundamental resonant frequency of her Achilles tendon?

in progress 0
Amity 4 years 2021-08-14T18:13:37+00:00 1 Answers 67 views 0

Answers ( )

  1. yenoanh
    0
    2021-08-14T18:14:39+00:00
    Reply

    Answer:

    161.9 Hz ( fundamental resonant frequency )

    other resonant frequencies: 323.85 Hz, 485.7 Hz..

    Explanation:

    Given:

    A= 130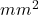 mm^{2} => 130 x 10^{-6} m^{2}

    Tension T= 600N

    Length L= 20cm= 0.2m

    Density of tendon ρ= 1100 kg/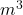m^{3}

    Linear mass density is defines as:

    μ = m/L =  ρV/ L =  ρAL / L

    μ = ρA

    where,

    m=mass , V = volume,  L= length , A= cross section area and ρ= density

    so, μ = 1100 x 130 x 10^{-6} => 0.143 kg/m

    Wave speed in the string is defines as

    v=  sqrt(T/μ)

    where,

    T is string tension and μ is the linear mass density.

    So,

    v=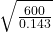  \sqrt{\frac{600}{0.143} }

    v= 64.77 m/s

    Frequencies of standing wave- modes of a string of length L fixed at both ends can be defines as:

    fm = m (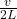\frac{v}{2L} )                where m= 1,2,3,4,…..

    Therefore,  fundamental resonant frequency of her Achilles tendon is:

    f_{1} =  \frac{64.77}{2 * 0.2} =>  161.9 Hz

    The other resonant frequencies can be find by integral multiples of frequence.

    So,

    f_{n} = n * f_{1}

    f_{2} = 2 * 161.9 = 323.85 Hz

    f_{3} = 3 * 161.9  = 485.7 Hz

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )