Share
Suppose the sand in a sand box with length 14 feet, width 8 feet, and height 1.5 feet is to be removed. The density of the sand (in pounds p
Question
Suppose the sand in a sand box with length 14 feet, width 8 feet, and height 1.5 feet is to be removed. The density of the sand (in pounds per cubic feet) h feet from the bottom is given by δ(h)=2.5−h. Find the work required to completely empty the sandbox.
in progress
0
Physics
4 years
2021-08-02T16:47:57+00:00
2021-08-02T16:47:57+00:00 1 Answers
42 views
0

Answers ( )
Answer:
The work required is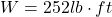
Explanation:
The volume of the sand box is mathematical represented as
Substituting 14 feet for L, 8 feet for W into the equation
The force as a result of the sand in the disk is mathematically represented as
Substituting (2.5-h) for
Now the work that is required to lift the sand from h = 0 to a height of h=1.5 m is mathematically represented as
Now above is the formula for change in work done in order to obtain the workdone we integrate