Suppose speeds of vehicles traveling on a highway have an unknown distribution with mean 63 and standard deviation 4 miles per hour. A sampl

Question

Suppose speeds of vehicles traveling on a highway have an unknown distribution with mean 63 and standard deviation 4 miles per hour. A sample of size n-44 is randomly taken from the population and the mean is taken. Using the Central Limit Theorem for Means, what is the standard deviation for the sample mean distribution?

in progress 0
Nick 4 years 2021-07-31T00:32:58+00:00 1 Answers 38 views 0

Answers ( )

  1. ngochoa
    0
    2021-07-31T00:34:10+00:00
    Reply

    Answer:

    The standard deviation for the sample mean distribution=0.603

    Step-by-step explanation:

    We are given that

    Mean,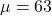\mu=63

    Standard deviation,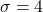\sigma=4

    n=44

    We have to find the standard deviation for the sample mean distribution using  Central Limit Theorem for Means.

    Standard deviation for the sample mean distribution

    \sigma_x=\frac{\sigma}{\sqrt{n}}

    Using the formula

    \sigma_x=\frac{4}{\sqrt{44}}

    \sigma_x=\frac{4}{\sqrt{2\times 2\times 11}}

    \sigma_x=\frac{4}{2\sqrt{11}}

    \sigma_x=\frac{2}{\sqrt{11}}

    \sigma_x=0.603

    Hence, the standard deviation for the sample mean distribution=0.603

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )