Suppose a wheel with a tire mounted on it is rotating at the constant rate of 2.23 2.23 times a second. A tack is stuck in the tire at a dis

Question

Suppose a wheel with a tire mounted on it is rotating at the constant rate of 2.23 2.23 times a second. A tack is stuck in the tire at a distance of 0.379 m 0.379 m from the rotation axis. Noting that for every rotation the tack travels one circumference, find the tack’s tangential speed

in progress 0
Maris 4 years 2021-08-28T07:08:42+00:00 1 Answers 6 views 0

Answers ( )

  1. thugiang
    0
    2021-08-28T07:10:00+00:00
    Reply

    Explanation:

    The given data is as follows.

           Angular velocity (\omega) = 2.23 rps

         Distance from the center (R) = 0.379 m

    First, we will convert revolutions per second into radian per second as follows.

                 = 2.23 revolutions per second

                 = 2.23 \times 2 \times 3.14 rad/s

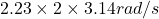
                 = 14.01 rad/s

    Now, tangential speed will be calculated as follows.

      Tangential speed, v =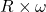 R \times \omega

                                   = 0.379 x 14.01

                                   = 5.31 m/s

    Thus, we can conclude that the tack’s tangential speed is 5.31 m/s.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )