Solve cos x + √2 = -cos x for x over the interval [0, 2Π)

Question

Solve cos x + √2 = -cos x for x over the interval [0, 2Π)

in progress 0
Dâu 4 years 2021-08-27T05:27:33+00:00 1 Answers 9 views 0

Answers ( )

  1. Ben
    0
    2021-08-27T05:29:10+00:00
    Reply

    Answer:

    x=\frac{3\pi}{4}\\\\x=\frac{5\pi}{4}

    Step-by-step explanation:

    Trigonometric Equations

    It’s required to solve:

    \cos x+\sqrt{2}=-\cos x

    for x\in [0,2\pi)

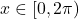
    Adding cos x:

    2\cos x+\sqrt{2}=0

    Subtracting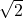 \sqrt{2}

    2\cos x=-\sqrt{2}

    Dividing by 2:

    \displaystyle \cos x=-\frac{\sqrt{2}}{2}

    Solving for x:

    \displaystyle x=\arccos\left(-\frac{\sqrt{2}}{2}\right)

    We need to find the angles whose cosine is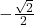 -\frac{\sqrt{2}}{2} over the given interval.

    These angles lie on the quadrants III and IV respectively and they are:

    x=135°, x=225°

    Converting to radians:

    135 * π / 180 = 3π/4

    225 * π / 180 = 5π/4

    The two solutions are:

    \mathbf{x=\frac{3\pi}{4}}

    \mathbf{x=\frac{5\pi}{4}}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )