What is the equation of the line that has a slope of 1/3 and goes through the point (6,−2)? A. y = 1/3x − 4 B. y = 1/3x +

Question

What is the equation of the line that has a slope of 1/3 and goes through the point (6,−2)?

A. y = 1/3x − 4
B. y = 1/3x + 4
C. y = 1/3x − 8
D. y = 1/3x

in progress 0
Minh Khuê 4 years 2021-09-01T01:59:45+00:00 1 Answers 10 views 0

Answers ( )

  1. ThanhThu
    0
    2021-09-01T02:01:22+00:00
    Reply

    Answer: A) y = 1/3x − 4

    Step-by-step explanation:

    Find the Equation Using Point-Slope Formula

    slope: 1/3

    point: (6, −2)

    Use the slope 1 and a given point (6, −2) to substitute for x_1  and y_1  in the point-slope form  

    y – y_1 = m(x – x_1), which is derived from the slope equation m = \frac{y_2-y_1}{x_2-x_1}

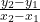
      y − (−2) = 1/3 ⋅ (x − (6))

    Simplify the equation and keep it in point-slope form.

      y + 2 = 1/3 ⋅ (x − 6)

    Solve for y.  

      1/3 ⋅ (x − 6).

    Apply the distributive property.

      y + 2 =  1
    /3 x +  1
    /3 ⋅ − 6

    Combine 1/3 and x.

      y + 2 =  x/3 +1/3 ⋅ −6

    Cancel the common factor of 3.

      y + 2 =  x
    /3 − 2

    Move all terms not containing y to the right side of the equation.

    Subtract 2 from both sides of the equation.

      y = x/3 − 2 − 2

    Subtract 2 from −2. x

      y = x/3 − 4

    Reorder terms.

      y = 1/3x − 4

    List the equation in different forms.

    Slope-intercept form:  

    y = 1/3x − 4

    Point-slope form:

    y + 2 = 1/3 ⋅ (x − 6)

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )