Water at 70 kPa flows through a horizontal 2 meter diameter pipe at a velocity of 71 m/s and an elevation of 54 meters. If the density of wa

Question

Water at 70 kPa flows through a horizontal 2 meter diameter pipe at a velocity of 71 m/s and an elevation of 54 meters. If the density of water is 1000 kg/m^3 and the specific weight is 9.8 kN/m^3, what is the total pressure? Round to the nearest kPa.

in progress 0
Khoii Minh 4 years 2021-08-22T17:18:31+00:00 1 Answers 7 views 0

Answers ( )

  1. Xavia
    0
    2021-08-22T17:20:00+00:00
    Reply

    Answer:

    The total pressure is 3120 kilopascals.

    Explanation:

    The total pressure of this water flow is determined by the Bernoulli’s Principle, which is the sum of dynamic (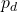p_{d}) and hydraulic pressure (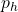p_{h}). That is:

    p_{T} = p_{d} + p_{h}

    p_{T} = \frac{1}{2}\cdot \rho \cdot v^{2} + \gamma \cdot z + p

    Where:

    \rho – Density, measured in kilograms per cubic meter.

    v – Flow velocity, measured in meters per second.

    \gamma – Specific weight, measured in newtons per cubic meter.

    z – Elevation, measured in meters.

    p – Static pressure, measured in pascals.

    Given that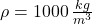 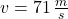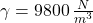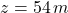\rho = 1000\,\frac{kg}{m^{3}}, v = 71\,\frac{m}{s}, \gamma = 9800\,\frac{N}{m^{3}}, z = 54\,m and p = 70000\,Pa, the total pressure is:

    p_{T} = \frac{1}{2}\cdot \left(1000\,\frac{kg}{m^{3}} \right)\cdot \left(71\,\frac{m}{s} \right)^{2} + \left(9800\,\frac{N}{m^{3}} \right)\cdot (54\,m)+70000\,Pa

    p_{T} = 3119700\,Pa

    p_{T} = 3119,7\,kPa (1 kPa = 1000 Pa)

    p_{T} = 3120\,kPa

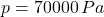    The total pressure is 3120 kilopascals.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )