Two identical wheels, wheel 1 and wheel 2, initially at rest begin to rotate with constant angular accelerations α. After rotating through t

Question

Two identical wheels, wheel 1 and wheel 2, initially at rest begin to rotate with constant angular accelerations α. After rotating through the same angular displacement, Δθ0, the angular velocity of wheel 1 is ω1 and the angular velocity of wheel 2 is ω2=3ω1. How does the angular acceleration of wheel 2, α2, compare to the angular acceleration of wheel 1, α1?a. a2 = a1b. a2 = a1/3c. a2 = 3a1d. a2 = 9a1

in progress 0
Verity 4 years 2021-07-14T09:05:58+00:00 1 Answers 34 views 0

Answers ( )

  1. thanhcong
    0
    2021-07-14T09:07:21+00:00
    Reply

    Answer:

    d. a2 = 9a1

    Explanation:

    We can apply the following equation of motion to calculate the angular acceleration:

    \omega^2 - \omega_0^2 = 2\alpha\theta

    Since both wheel starts from rest, their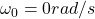 \omega_0 = 0 rad/s

    \omega^2 = 2\alpha\theta

    We can take the equation for the 1st wheel, divided by the equation by the 2nd wheel:

    \frac{\omega_1^2}{\omega_2^2} = \frac{2\alpha_1\theta_1}{2\alpha_2\theta_2}

    As they were rotating through the same angular displacement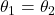 \theta_1 = \theta_2, these 2 cancel out

    \left(\frac{\omega_1}{\omega_2}\right)^2 = \frac{\alpha_1}{\alpha_2}

    \left(\frac{1}{3}\right)^2 = \frac{\alpha_1}{\alpha_2}

    \frac{1}{9} = \frac{\alpha_1}{\alpha_2}

    \alpha_2 = 9\alpha_1

    So d is the correct answer

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )