Share
Two Carnot heat engines are operating in series such that the heat sink of the first engine serves as the heat source of the second on. If t
Question
Two Carnot heat engines are operating in series such that the heat sink of the first engine serves as the heat source of the second on. If the source temperature of the first engine is 1300 K and the sink temperature of the second engine is 300 K and the thermal efficiencies of both engines are the same, the temperature of the intermediate reservoir is
in progress
0
Physics
4 years
2021-09-05T06:22:57+00:00
2021-09-05T06:22:57+00:00 1 Answers
30 views
0

Answers ( )
Answer:
the temperature of the intermediate reservoir is 624.5 K
Explanation:
Given the data in the question
The two Carnot heat engines are operating in series;
[ T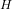 ]
]
↓
((1)) ⇒ W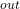
↓
[ T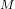 ]
]
↓
((2)) ⇒ W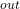
[ T ]
]
The maximum possible efficiency for any heat engine is the Carnot efficiency;
η = 1 –
= 1 – 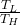
the thermal efficiencies if both engines are the same will be;
η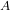 = η
= η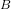
1 –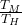 = 1 –
= 1 – 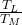
1 – 1 –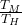 = –
= – 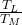
–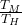 = –
= – 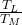
T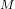 ² = T
² = T × T
× T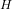
T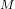 = √(T
= √(T × T
× T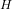 )
)
source temperature of the first engine T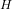 = 1300 K
= 1300 K
sink temperature of the second engine T = 300 K
= 300 K
we substitute
T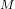 = √(300 × 1300)
= √(300 × 1300)
T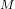 = √390000
= √390000
T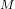 = 624.4998 K ≈ 624.5 K
= 624.4998 K ≈ 624.5 K
Therefore, the temperature of the intermediate reservoir is 624.5 K