The fracture strength of a certain type of manufactured glass is normally distributed with a mean of 509 MPa with a standard deviation of 17

Question

The fracture strength of a certain type of manufactured glass is normally distributed with a mean of 509 MPa with a standard deviation of 17 MPa. (a) What is the probability that a randomly chosen sample of glass will break at less than 509 MPa

in progress 0
Helga 4 years 2021-08-05T08:43:09+00:00 1 Answers 20 views 0

Answers ( )

  1. Edana
    0
    2021-08-05T08:45:06+00:00
    Reply

    Answer:

    0.5 = 50% probability that a randomly chosen sample of glass will break at less than 509 MPa

    Step-by-step explanation:

    Normal Probability Distribution

    Problems of normal distributions can be solved using the z-score formula.

    In a set with mean \mu and standard deviation \sigma, the z-score of a measure X is given by:

    Z = \frac{X - \mu}{\sigma}

    The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

    Mean of 509 MPa with a standard deviation of 17 MPa.

    This means that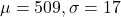 \mu = 509, \sigma = 17

    What is the probability that a randomly chosen sample of glass will break at less than 509 MPa?

    This is the p-value of Z when X = 509. So

    Z = \frac{X - \mu}{\sigma}

    Z = \frac{509 - 509}{17}

    Z = 0

    Z = 0 has a p-value of 0.5

    0.5 = 50% probability that a randomly chosen sample of glass will break at less than 509 MPa

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )