Share
Suppose that a wing component on an aircraft is fabricated from an aluminum alloy that has a plane strain fracture toughness of 29 MPa (26.3
Question
Suppose that a wing component on an aircraft is fabricated from an aluminum alloy that has a plane strain fracture toughness of 29 MPa (26.39 ksi). It has been determined that fracture results at a stress of 118 MPa (17110 psi) when the maximum internal crack length is 8.7 mm (0.3425 in.). For this same component and alloy, compute the stress level at which fracture will occur for a critical internal crack length of 5.9 mm (0.2323 in.).
in progress
0
Physics
4 years
2021-09-05T04:14:29+00:00
2021-09-05T04:14:29+00:00 1 Answers
37 views
0

Answers ( )
Answer:
Suppose that a wing component on an aircraft is fabricated from an aluminum alloy that has a plane-strain fracture toughness of 26.0 MPa m−−√
(23.7 ksi in.−−√
). It has been determined that fracture results at a stress of 112 MPa (16,240 psi) when the maximum internal crack length is 8.6 mm (0.34 in.). For this same component and alloy, compute the stress level at which fracture will occur for a critical internal crack length of 6.0 mm (0.24 in.).
Explanation:
As we know
σ =
= 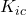 / y√π a
/ y√π a
y =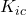 / σ
/ σ √π a
√π a
y =![Rendered by QuickLaTeX.com \frac{{29 MPa} }{(118 MPa)\sqrt{(3.14)[\frac{8.7*10^{-2} }{2}] } }](https://documen.tv/wp-content/ql-cache/quicklatex.com-f322d46395fc18aaed689d170027d5a9_l3.png)
y = 2.00
now,
σ =
= 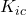 / y√π a
/ y√π a
=![Rendered by QuickLaTeX.com \frac{{29 MPa} }{( 2.00)\sqrt{(3.14)[\frac{5.9*10^{-3} }{2}] } }](https://documen.tv/wp-content/ql-cache/quicklatex.com-b7ab220f1e55895b28cfa99a4d21601e_l3.png)
= 150.65 MPa
So the stress level at which the fracture will occur for acritical internal crack length of 5.9 mm is 150.65 MPa.