State the common factor of the terms in the polynomial 5x^2 + 30x^2 – 10x. Then factor the polynomial

Question

Question

in progress 0

Mathematics Thạch Thảo 3 years 2021-07-16T04:43:14+00:00 2021-07-16T04:43:14+00:00 1 Answers 1 views 0

Answers ( )

Name*

E-Mail*

Website

Featured image

Browse

Captcha* Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )

Answer*

huyenthanh · Answer 1 · 2021-07-16T04:44:49+00:00

Answer:

The common factor is 5x.

The factored polynomial is: $5x(7x - 2)$

Step-by-step explanation:

Factor of the numbers:

The common factor of the numbers 5, 30 and 10 is 5, as it is the greater common divisor of them, as found below:

5 – 30 – 10|5

1 – 6 – 2

Factor of the exponents:

Between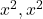 $x^2, x^2$ and $x$ , the common factor is the x with the lowest exponent. So x

Common factor

Number multiplied by exponents, so 5x.

Factoring the polynomial:

$5x^2 + 30x^2 - 10x = 5x(\frac{5x^2}{5x} + \frac{30x^2}{5x} - \frac{10x}{5x}) = 5x(x + 6x - 2) = 5x(7x - 2)$

The factored polynomial is: $5x(7x - 2)$