Pour into a container with a longitudinal expansion coefficient of five times ten to the negative power of five, a liquid with a longitudina

Question

Pour into a container with a longitudinal expansion coefficient of five times ten to the negative power of five, a liquid with a longitudinal expansion coefficient of three to fifty-five hundredths multiplied by ten to the negative power of four. Increase the temperature of the set by a few degrees Kelvin to increase the height of the liquid inside the container by five percent? (Liquid does not spill out of the container)

in progress 0
Thiên Di 4 years 2021-09-03T14:50:18+00:00 1 Answers 12 views 0

Answers ( )

  1. Gerda
    0
    2021-09-03T14:52:00+00:00
    Reply

    Answer:

     ΔT = 200ºC to  ΔT = 11ºC

    Explanation:

    This is a thermal expansion exercise, for a material with volume the expression

              ΔV = β V₀ ΔT

    for when the changes are small

             β = 3 aα

    in the exercise they indicate the coefficient of thermal expansion of the liquid and solid

             α_solid = 5 10⁻⁵ ºC⁻¹

             α_liquid = 3 to 55 10⁻⁴ ºC⁻¹ = 30 to 550 10⁻⁵ ºC⁻¹

    it is requested to increase the temperature so that the height of the liquid rises 5% = 0.05 inside the container

    The expression for the volume of a body is its area for the height

            V₀ = π r² h

    the final volume when heated changes as the radius and height change, suppose the radius is equal to the height

            r = h

            V_f = π (h + 0.05h)² (h + 0.05)

            V_f = pi h² 1,05³

         

            V_f = 1.157525 V₀

    the volume variation is

             V_f – V₀ = 1.15 V₀ – V₀

             ΔV = 0.15 V₀

    therefore, so that the total change in the volume of liquid and solid is the desired

             ΔV = ΔV_{liquid} – ΔV_{solid}

    let’s write the dilation equations for the two elements

             ΔV_{liquid} = 3 α_{liquid} V₀ ΔT

             ΔV_{solid} =  3 α_{solid} V₀ ΔT

    we are assuming that the volumes of the solid and liquid are initial, as well as their temperatures

    we substitute

              0.15 V₀ = 3 α_{liquid} V₀ ΔT – 3 α_{solid} V₀ ΔT

              0.15 = 3 ΔT ( α_{liquid} – α_{solid})

              ΔT =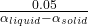 \frac{0.05}{\alpha_{liquid} - \alpha_{solid} }

    let’s calculate for the extreme values ​​of the liquid

    α_{liquid} = 30 10⁻⁵ ºC⁻¹

              ΔT =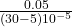 \frac{0.05}{( 30 -5 ) 10^{-5}}

              ΔT = 5000/25

              ΔT = 200ºC

    α_{liquid} = 5.5 10-5

               ΔT = \frac{0.05}{( 550 -5 ) 10^{-5}}

               ΔT = 5000 / 450

               ΔT = 11ºC

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )