Share
integrate G(x,y,z)=yz over the surface of x+y+z=1 in the first octant.
Question
integrate G(x,y,z)=yz over the surface of x+y+z=1 in the first octant.
in progress
0
Mathematics
3 years
2021-07-25T20:04:28+00:00
2021-07-25T20:04:28+00:00 1 Answers
16 views
0

Answers ( )
Parameterize the surface (I’ll call it S) by
r(u, v) = (1 – u) (1 – v) i + u (1 – v) j + v k
with 0 ≤ u ≤ 1 and 0 ≤ v ≤ 1.
Take the normal vector to this surface to be
n = ∂r/∂u × ∂r/∂v = ((v – 1) i + (1 – v) j) × ((u – 1) i – u j + k) = (1 – v) (i + j + k)
with magnitude
||n|| = √3 (1 – v)
Then in the integral, we have
Alternatively, if you’re not familiar with parameterizing surfaces, you can use the “projection” formula:
where I write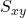 to mean the projection of the surface onto the (x, y)-plane, and z = f(x, y). We would then use
to mean the projection of the surface onto the (x, y)-plane, and z = f(x, y). We would then use
x + y + z = 1 ==> z = f(x, y) = 1 – x – y
and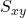 is the triangle,
is the triangle,
{(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 – x}
Then the integral becomes