Share
In ΔXYZ, y = 75 cm, z = 83 cm and ∠X=157°. Find the length of x, to the nearest centimeter.
Question
In ΔXYZ, y = 75 cm, z = 83 cm and ∠X=157°. Find the length of x, to the nearest centimeter.
in progress
0
Mathematics
4 years
2021-08-05T16:52:06+00:00
2021-08-05T16:52:06+00:00 1 Answers
52 views
0

Answers ( )
Answer:
x = 155 cm
Step-by-step explanation:
The Law of Cosines
It relates the length of the sides of a triangle with one of its internal angles.
Let x,y, and z be the length of the sides of a given triangle, and X the included angle between sides y and z, then the following relation applies:
It’s given: y=75 cm, z=83 cm, and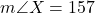 °
°
. Applying the formula:
Calculating:
x = 155 cm