Share
In AWXY, the measure of ZY=90°, WY = 5, XW = 13, and YX = 12. What ratio represents the cosine of ZW?
Question
In AWXY, the measure of ZY=90°, WY = 5, XW = 13, and YX = 12. What ratio
represents the cosine of ZW?
in progress
0
Mathematics
3 years
2021-08-18T23:35:25+00:00
2021-08-18T23:35:25+00:00 1 Answers
37 views
0

Answers ( )
Given:
In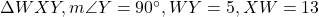 and
and 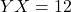 .
.
To find:
The ratio represents the cosine of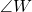 .
.
Solution:
In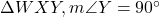 . It means the opposite side of angle Y, i.e., XW is the hypotenuse of the triangle.
. It means the opposite side of angle Y, i.e., XW is the hypotenuse of the triangle.
In a right angle triangle,
In the given triangle,
Therefore, the required cosine ratio is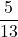 .
.