Share
In a home stereo system, low sound frequencies are handled by large “woofer” speakers, and high frequencies by smaller “tweeter” speakers. F
Question
In a home stereo system, low sound frequencies are handled by large “woofer” speakers, and high frequencies by smaller “tweeter” speakers. For the best sound reproduction, low-frequency currents from the amplifier should not reach the tweeter. One way to do this is to place a capacitor in series with the 9.0 Ω resistance of the tweeter; one then has an RLC circuit with no inductor L (that is, an RLC circuit with L = 0).
What value of C should be chosen so that the current through the tweeter at 200 Hz is half its value at very high frequencies? Express your answer with the appropriate units.
in progress
0
Physics
4 years
2021-09-01T01:24:15+00:00
2021-09-01T01:24:15+00:00 1 Answers
33 views
0

Answers ( )
Answer:
C = 2.9 10⁻⁵ F = 29 μF
Explanation:
In this exercise we must use that the voltage is
V = i X
i = V/X
where X is the impedance of the system
in this case they ask us to treat the system as an RLC circuit in this case therefore the impedance is
X =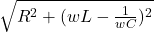
tells us to take inductance L = 0.
The angular velocity is
w = 2π f
the current is required to be half the current at high frequency.
Let’s analyze the situation at high frequency (high angular velocity) the capacitive impedance is very small
therefore in this frequency regime
X₀ =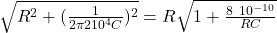
the very small fraction for which we can despise it
X₀ = R
to halve the current at f = 200 H, from equation 1 we obtain
X = 2X₀
let’s write the two equations of inductance
X₀ = R w → ∞
X= 2X₀ =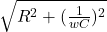 w = 2π 200
w = 2π 200
we solve the system
2R = \sqrt{R^2 +( \frac{1}{wC} )^2 }
4 R² = R² + 1 / (wC) ²
1 / (wC) ² = 3 R²
w C =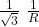
C =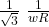
let’s calculate
C =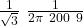
C = 2.9 10⁻⁵ F
C = 29 μF