- Tumblr
-
, then show that
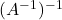 ">
, then show that
">
, then show that 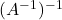 " target="_blank">Pinterest
" target="_blank">Pinterest
-
, then show that
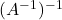 &body=https://documen.tv/question/if-a-te-left-begin-array-ccc-cos-sin-sin-cos-end-array-right-te-then-show-that-te-a-1-1-te-24160735-2/', 'PopupPage', 'height=450,width=500,scrollbars=yes,resizable=yes'); return false" href="#">
, then show that
&body=https://documen.tv/question/if-a-te-left-begin-array-ccc-cos-sin-sin-cos-end-array-right-te-then-show-that-te-a-1-1-te-24160735-2/', 'PopupPage', 'height=450,width=500,scrollbars=yes,resizable=yes'); return false" href="#">
, then show that 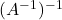 &body=https://documen.tv/question/if-a-te-left-begin-array-ccc-cos-sin-sin-cos-end-array-right-te-then-show-that-te-a-1-1-te-24160735-2/', 'PopupPage', 'height=450,width=500,scrollbars=yes,resizable=yes'); return false" href="#">Email
&body=https://documen.tv/question/if-a-te-left-begin-array-ccc-cos-sin-sin-cos-end-array-right-te-then-show-that-te-a-1-1-te-24160735-2/', 'PopupPage', 'height=450,width=500,scrollbars=yes,resizable=yes'); return false" href="#">Email
Share

Answers ( )
Given:
The matrix is:
To show:
Solution:
If a matrix is:
Then,
We have,
Using the above formula, we get
Now, the inverse of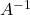 is:
is:
Hence proved.