Share
Find the value of 373 using the identity (x − y)3 = x3 − 3x2y + 3xy2 − y3. Show all work. Hint: 373 = (40 − 3)3; therefore
Question
Find the value of 373 using the identity (x − y)3 = x3 − 3x2y + 3xy2 − y3. Show all work.
Hint: 373 = (40 − 3)3; therefore, x = 40 and y = 3.
in progress
0
Mathematics
4 years
2021-08-09T10:52:52+00:00
2021-08-09T10:52:52+00:00 1 Answers
20 views
0

Answers ( )
Answer:
Step-by-step explanation:
Given
Required
Find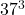
Express 37 as 40 – 3
So, we have:
Compare to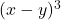
Substitute 40 for x and 3 for y in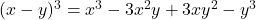
Evaluate all exponents
Evaluate all products
Hence: