Determine whether the following equation represents a direct variation If it does, find the constant of variation 2x + 3y = 0

Question

Question

Determine whether the following equation represents a direct variation If it does, find the constant of variation
2x + 3y = 0

in progress 0

Mathematics Khoii Minh 4 years 2021-09-04T11:24:59+00:00 2021-09-04T11:24:59+00:00 1 Answers 19 views 0

Answers ( )

Name*

E-Mail*

Website

Featured image

Browse

Captcha* Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )

Answer*

Jezebel · Answer 1 · 2021-09-04T11:26:37+00:00

Given:

The equation is

$2x+3y=0$

To find:

Whether the equation represents a direct variation. If it does, find the constant of variation.

Solution:

The general equation of direct variation is

$y=kx$ …(i)

Where, k is the constant of variation.

The equation of direct variation is always true for (0,0).

The given equation is

$2x+3y=0$

It can be written as

$3y=-2x$

$y=-\dfrac{2}{3}x$ …(ii)

For x=0,

$y=-\dfrac{2}{3}(0)$

$y=0$

The given equation is true for (0,0). So, it represents a direct variation.

On comparing (i) and (ii), we get

$k=-\dfrac{2}{3}$

Therefore, the constant of variation is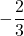 $-\dfrac{2}{3}$ .