Share
At 298 K, the rate constant for a reaction is 0.0346 s-1. What is the rate constant at 350K if the Ea = 50.2kJ/mol
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Answer:
0.702 /s
Explanation:
Rate constant at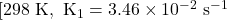
Rate constant at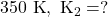
Activation energy,
Use the following equation to calculate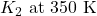
Use the following equation to calculate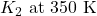
Therefore,
hence, the rate constant at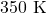 is 0.702
is 0.702