As an aid in working this problem, consult Interactive Solution 3.41. A soccer player kicks the ball toward a goal that is 25.0 m in front o

Question

As an aid in working this problem, consult Interactive Solution 3.41. A soccer player kicks the ball toward a goal that is 25.0 m in front of him. The ball leaves his foot at a speed of 16.2 m/s and an angle of 38.0 ° above the ground. Find the speed of the ball when the goalie catches it in front of the net.

in progress 0
Amity 4 years 2021-08-09T12:25:42+00:00 1 Answers 11 views 0

Answers ( )

  1. ngocdiep
    0
    2021-08-09T12:27:27+00:00
    Reply

    Answer:

    15.77m/s

    Explanation:

    the information we have is:

    initial velocity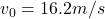 v_{0}=16.2m/s

    distance: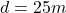 d=25m

    angle: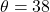 \theta=38°

    first we need to break down the velocity into its x and y components:

    initial velocity in x (the velocity in x is constant):

    v_{0x}=v_{0}cos\theta\\v_{0x}=(16.2m/s)cos38\\v_{0x}=12.766m/s

    and initial velocity in y (the velocity in y is not constant due to acceleration of gravity):

    v_{0y}=v_{0}sin\theta\\v_{0y}=(16.2m/s)sin38\\v_{0y}=9.97m/s

    and now we find the time that the ball was in the air:

    t=\frac{d}{v_{0x}} =\frac{25m}{12.766m/s}\\ t=1.96s

    and with this time, we find the y component of the volicity at time 1.96s:

    v_{y}=v_{0y}-gt\\v_{y}=(9.97m/s)-(9.81m/s^2)(1.96s)\\v_{y}=-9.26m/s(negative because it points downward)

    finally, to find the final velocity we use pythagoras:

    v_{f}=\sqrt{v_{x}^2+v_{y}^2} =\sqrt{12.766^2+(-9.26)^2}=15.77m/s

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )