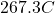Argon gas enters steadily an adiabatic turbine at 900 kPa and 450C with a velocity of 80 m/s and leaves at 150 kPa with a velocity of 150 m

Question

Argon gas enters steadily an adiabatic turbine at 900 kPa and 450C with a velocity of 80 m/s and leaves at 150 kPa with a velocity of 150 m/s. The inlet area of the turbine is 60 cm2. If the power output of the turbine is 250 kW, determine the exit temperature of the argon.

in progress 0
Ngọc Khuê 4 years 2021-08-05T20:04:53+00:00 1 Answers 589 views 0

Answers ( )

  1. RuslanHeatt
    0
    2021-08-05T20:06:29+00:00
    Reply

    Answer:

    Temperature at the exit =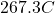 267.3 C

    Explanation:

    For the steady energy flow through a control volume, the power output is given as

    W_{out}= -m_{f}(h_{2}-h_{1} + \frac{v_{2}^{2}}{2} - \frac{v_{1}^{2}}{2})

    Inlet area of the turbine =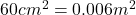 60cm^{2}= 0.006m^{2}

    To find the mass flow rate, we can apply the ideal gas laws to estimate the specific volume, from there we can get the mass flow rate.

    Assuming Argon behaves as an Ideal gas, we have the specific volume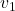 v_{1}

    as

    v_{1}=\frac{RT_{1}}{P_{1}}=\frac{0.2081\times723}{900}=0.1672m^{3}/kg

    m_{f}=\frac{1}{v_{1}}\times A_{1}V_{1} = \frac{1}{0.1672}\times(0.006)(80)=2.871kg/sec

    for Ideal gasses, the enthalpy change can be calculated using the formula

    h_{2}-h_{1}=C_{p}(T_{2}-T_{1})

    hence we have

    W_{out}= -m_{f}((C_{p}(T_{2}-T_{1}) + \frac{v_{2}^{2}}{2} - \frac{v_{1}^{2}}{2})

    250= -2.871((0.5203(T_{2}-450) + \frac{150^{2}}{2\times 1000} - \frac{80^{2}}{2\times 1000})

    Note: to convert the Kinetic energy term to kilojoules, it was multiplied by 1000

    evaluating the above equation, we have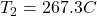 T_{2}=267.3C

    Hence, the temperature at the exit = 267.3 C

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )