Share
An object, with mass 64 kg and speed 14 m/s relative to an observer, explodes into two pieces, one 2 times as massive as the other; the expl
Question
An object, with mass 64 kg and speed 14 m/s relative to an observer, explodes into two pieces, one 2 times as massive as the other; the explosion takes place in deep space. The less massive piece stops relative to the observer. How much kinetic energy is added to the system during the explosion, as measured in the observer’s reference frame
in progress
0
Physics
4 years
2021-09-03T07:23:41+00:00
2021-09-03T07:23:41+00:00 1 Answers
12 views
0

Answers ( )
Answer:
K_f = 1881.6 J
Explanation:
To solve this exercise, let’s start by finding the velocities of the bodies.
We define a system formed by the initial object and its parts, with this the forces during the explosion are internal and the moment is conserved
initial instant. Before the explosion
p₀ = M v₀
final instant. After the explosion
p_f = m₁ v + m₂ 0
the moeoto is preserved
p₀ = p_f
M v₀ = m₁ v
v =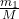 v₀
v₀
in the exercise they indicate that the most massive part has twice the other part
M = m₁ + m₂
M = 2m₂ + m₂ = 3 m₂
m₂ = M / 3
so the most massive part is worth
m₁ = 2 M / 3
we substitute
v = ⅔ v₀
with the speed of each element we can look for the kinetic energy
initial
K₀ = ½ M v₀²
Final
K_f = ½ m₁ v² + 0
K_f = ½ (⅔ M) (⅔ v₀)²
K_f =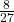 (½ M v₀²)
(½ M v₀²)
K_f =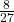 K₀
K₀
the energy added to the system is
ΔK = Kf -K₀
ΔK = (8/27 – 1) K₀
ΔK = -0.7 K₀
K_f = K₀ + ΔK
K_f = K₀ (1 -0.7)
K_f = 0.3 K₀
let’s calculate
K_f = 0.3 (½ 64 14²)
K_f = 1881.6 J