An object floats in water with 58 of its volume submerged. The ratio of the density of the object to that of water is

Question

Question

in progress 0

Physics Orla Orla 4 years 2021-08-07T05:49:12+00:00 2021-08-07T05:49:12+00:00 1 Answers 8 views 0

Answers ( )

Name*

E-Mail*

Website

Featured image

Browse

Captcha* Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )

Answer*

Eirian · Answer 1 · 2021-08-07T05:51:09+00:00

Complete Question

An object floats in water with 5/8 of its volume submerged. The ratio of the density of the object to that of water is:

(a) 8/5

(b) 1/2

(c) 3/8

(d) 5/8

(e) 2/1

Answer:

The correct option is d

Explanation:

From the question we are told that

The ratio of the volume of the object submerged to the total volume of the object is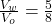 $\frac{V_w}{V_o} = \frac{5}{8}$

Generally the buoyancy force acting on the object is equal to the weight of the water displaced and this is mathematically represented as

$F_b = W$

Now the mass of the water displaced is mathematically represented as

$m_w = \rho_w * V_w$

While the mass of the object is mathematically represented as

$m_o = \rho_o * V_o$

So

$F_b = W \ \equiv \ \rho * V_o * g = \rho * V_w * g$

=> $\frac{V_w}{V_o} = \frac{\rho_o}{\rho_w}$

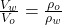
From the question that it volume of the water displace (equivalent to the volume of the object in water ) to the volume of the total object is

$\frac{V_w}{V_o} = \frac{5}{8}$

So

$\frac{\rho_o}{\rho_w} = \frac{5}{8}$