An element with mass 510 grams decays by 26.3% per minute. How much of the element is remaining after 7 minutes, to the nearest

Question

Question

An element with
mass 510 grams decays by 26.3% per minute. How much of the
element is remaining after 7 minutes, to the nearest 10th of a gram?

in progress 0

Mathematics Trúc Chi 4 years 2021-08-14T19:08:17+00:00 2021-08-14T19:08:17+00:00 1 Answers 8 views 0

Answers ( )

Name*

E-Mail*

Website

Featured image

Browse

Captcha* Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )

Answer*

danthu · Answer 1 · 2021-08-14T19:09:31+00:00

Answer:

60.2 grams is remaining after 7 minutes.

Step-by-step explanation:

Exponential equation for amount of substance:

The exponential equation for the amount of a substance is given by:

$A(t) = A(0)(1-r)^t$

In which A(0) is the initial amount and r is the decay rate, as a decimal, and t is the time measure.

An element with mass 510 grams decays by 26.3% per minute.

This means that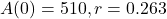 $A(0) = 510, r = 0.263$

So

$A(t) = A(0)(1-r)^t$

$A(t) = 510(1-0.263)^t$

$A(t) = 510(0.737)^t$

How much of the element is remaining after 7 minutes?

This is A(7). So

$A(7) = 510(0.737)^7 = 60.2$

60.2 grams is remaining after 7 minutes.