An electron is released from rest at the negative plate of a parallel plate capacitor. The charge per unit area on each plate is = 2.5 x 10⁻

Question

An electron is released from rest at the negative plate of a parallel plate capacitor. The charge per unit area on each plate is = 2.5 x 10⁻⁷ C/m², and the plates are separated by a distance of 1.7 x 10⁻² m. How fast is the electron moving just before it reaches the positive plate?

in progress 0
Thu Cúc 4 years 2021-08-25T05:21:58+00:00 1 Answers 29 views 0

Answers ( )

  1. ngockhue
    0
    2021-08-25T05:23:20+00:00
    Reply

    The speed of the electron before reaching the positive plate is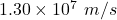 1.30 \times 10^{7}\ m / s

    Explanation:

    As per Gauss law of electro statistics, the electric field generated by a capacitor is directly proportional to the surface charge density of the plate and inversely proportional to the dielectric constant. In simple words, the electric field is proportional to the surface charge density.  So,  

        \text {Electric field}=\frac{\sigma}{\varepsilon_{0}}

    And then from the second law of motion,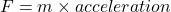 F=m \times acceleration

    So acceleration exerted by the electrons will be directly proportional to the force exerted on them and inversely proportional to the mass of the electron.

            Acceleration =\frac{F}{m}

    Since force is also calculated as product of charge with electric field in electrostatic force,

           \text {Acceleration}=\frac{q E}{m}=\frac{q \sigma}{m \varepsilon_{0}}

    So, the charge of electron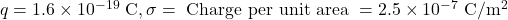q=1.6 \times 10^{-19}\ \mathrm{C}, \sigma=\text { Charge per unit area }=2.5 \times 10^{-7}\ \mathrm{C} / \mathrm{m}^{2}

    m is the mass of electron which is equal to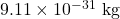 9.11 \times 10^{-31}\ \mathrm{kg}

    \varepsilon_{0}=8.85 \times 10^{-12}\ \mathrm{Nm}^{2} \mathrm{C}^{-2}

    Then,

        \text { Acceleration }=\frac{1.6 \times 2.5 \times 10^{-19} \times 10^{-7}}{9.11 \times 8.85 \times 10^{-31} \times 10^{-12}}=\frac{4 \times 10^{-19-7}}{80.62 \times 10^{-31-12}}

       \text { Acceleration }=0.0496 \times 10^{-19-7+31+12}=0.0496 \times 10^{17}\ \mathrm{m} / \mathrm{s}^{2}

    So the acceleration of the electron in the capacitor will be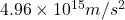 4.96 \times 10^{15} m / s^{2}

    Then, the velocity can be observed from the third equation of motion.

        v^{2}=u^{2}+2 a s

    As u = 0 and s is the distance of separation between two plates.

       \begin{array}{c}v^{2}=0+\left(2 \times 4.96 \times 10^{15} \times 1.7 * 10^{-2}\right) \\v^{2}=16.864 \times 10^{15-2}=16.864 \times 10^{13}=1.684 \times 10^{14}\end{array}

    Thus, v=\sqrt{\left(1.68 \times 10^{14}\right)}=1.30 \times 10^{7}\ m/s

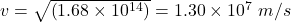
    So, the speed of the electron before reaching the positive plate is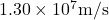 1.30 \times 10^{7} \mathrm{m} / \mathrm{s}.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )