An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude

Question

An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 29 inches, and the length of the base is 18 inches. Find the triangle’s perimeter. Round to the nearest tenth of an inch.

in progress 0
Thiên Thanh 4 years 2021-07-24T13:06:16+00:00 1 Answers 410 views 0

Answers ( )

  1. thaiduong
    0
    2021-07-24T13:08:01+00:00
    Reply

    Answer:

    Perimeter = 78.7 inches

    Step-by-step explanation:

    From the given question, applying the Pythagoras theorem to one of the congruent triangles formed, we have;

    /hyp/^{2} = /adj 1/^{2} + /adj 2/^{2}

              = (29)^{2} + (9)^{2}

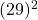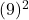
              =841 + 81

    /hyp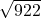/^{2} = 922

    hyp = \sqrt{922}

          = 30.3645

    The perimeter of the triangle can be determined as;

    perimeter =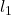 l_{1} + l_{2} + l_{3}

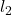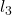
                     = 30.3645 + 18 + 30.3645

                     = 78.729

    The perimeter of the triangle = 78.7 inches

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )