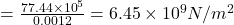Share
After a fall, a 75 kg rock climber finds himself dangling from the end of a rope that had been 18 m long and 11 mm in diameter but has stret
Question
After a fall, a 75 kg rock climber finds himself dangling from the end of a rope that had been 18 m long and 11 mm in diameter but has stretched by 2.1 cm. For the rope, calculate (a) the strain, (b) the stress, and (c) the Young’s modulus.
in progress
0
Physics
4 years
2021-07-25T13:46:25+00:00
2021-07-25T13:46:25+00:00 1 Answers
22 views
0

Answers ( )
Answer:
(A) Strain = 0.0012
(b) Stress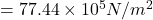
(c) Young’s modulus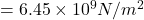
Explanation:
Mass of the rock m = 75 kg
So weight of the rock
Length of the rope l = 18 m
Diameter of the rope d = 11 mm
Change in length of rope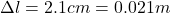
So radius r = 5.5 mm = 0.0055 m
Cross sectional area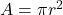
(a) Strain is equal to ratio change in length to original length
So strain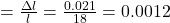
(b) Stress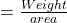
(c) Young’s modulus is equal to ratio of stress and strain
So young’s modulus