A student standing on a stationary skateboard tosses a textbook with a mass of mb = 1.95 kg to a friend standing in front of him. The studen

Question

A student standing on a stationary skateboard tosses a textbook with a mass of mb = 1.95 kg to a friend standing in front of him. The student and the skateboard have a combined mass of mc = 86 kg and the book leaves his hand at a velocity of vb = 4.54 m/s at an angle of 38° with respect to the horizontal.

in progress 0
Maris 4 years 2021-08-05T21:00:02+00:00 2 Answers 133 views 0

Answers ( )

  1. danthu
    1
    2021-08-05T21:01:47+00:00
    Reply

    Complete Question

    A student standing on a stationary skateboard tosses a textbook with a mass of mb = 1.95 kg to a friend standing in front of him. The student and the skateboard have a combined mass of mc = 86 kg and the book leaves his hand at a velocity of vb = 4.54 m/s at an angle of 38° with respect to the horizontal.

    a)Write an equation for the magnitude of the velocity of the student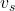 v_s after throwing the book

    b) Calculate the magnitude of the velocity of the student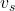 v_s in meter per second

    c What is the magnitude of the momentum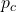 p_c which was transferred from the skateboard to the Earth during the time the book is being thrown in kilogram meter per second

    Answer:

    a

    The Equation is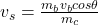 v_s = \frac{m_bv_b cos \theta}{m_c}

    b

    The magnitude of the for the velocity of the student is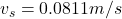  v_s= 0.0811 m/s

    c

    The momentum is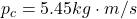  p_c =5.45kg \cdot m/s

    Explanation:

    From the question e are told that

           mass of the text book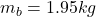 m_b = 1.95kg

           mass of student and skateboard is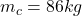 m_c =86kg

          The initial velocity of the book  is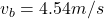 v_b = 4.54m/s

             The angle made is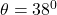  \theta = 38^0

    From the law of conservation of momentum along horizontal direction this can be mathematically represented as

               m_b v_b cos \theta = m_c v_c

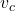    Making v_c the subject

                  v_c = \frac{m_bv_bcos \theta}{m_c}

    Since the total velocity of the skateboard and the student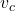 v_c would also be the velocity of the of the student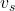 v_s

    Hence

                v_c = v_s = \frac{m_bv_b cos \theta}{m_c}

    Now substituting values

                 v_s = \frac{(1.95 *4,54 ) cos (38)}{86}

                     v_s= 0.0811 m/s

    The magnitude of the momentum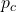 p_c is mathematically represented as

                       p_c = m_b v_b sin \theta

    Here this momentum is acting vertically opposite which is indicated by the resolution for the momentum to the vertical component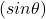 (sin \theta )

                     Substituting values

                               p_c = (1.95 ) (4.54) sin38

                                   p_c =5.45kg \cdot m/s

                 

               

  2. Nick
    0
    2021-08-05T21:01:59+00:00
    Reply

    The question is not complete. The missing part of the question says;

    a)Calculate the magnitude of the velocity of the student, v_s in meters per second.

    b)What is the magnitude of the momentum, pe, which was transferred from the skateboard to the the Earth during the time the book is being thrown (in kilogram meters per second)?

    Answer:

    A) v_s = 0.081 m/s in an opposite direction to that of the book.

    B) P_e = 5.45 Kg.m/s in downward direction.

    Explanation:

    We are given;

    Mass of the book m_b = 1.95 kg

    Mass of the student and the skateboard m_c = 86 kg

    Velocity of the book v_b = 4.54 m/s

    Angle of projection θ = 38°

    A) Using principle of conservation of momentum;

    The horizontal component of the velocity of book is given as;

    V_bx = V_b cos θ

    Now, the book and the student are initially at rest, and so their initial momentum is zero in both horizontal and vertical direction.

    Thus,

    Initial momentum = final momentum

    0 = m_b•v_b•cos θ + m_c•v_s

    Let’s make v_s the subject of the formula;

    v_s = -[m_b•v_b•cos θ]/m_c

    Plugging in the relevant values to get ;

    v_s = -[1.95•4.54•cos 38]/86

    v_s = -0.081 m/s

    The minus sign indicates that the direction of the velocity of the student is opposite to that of the book.

    B) The vertical component of the velocity of book is given as;

    V_by = V_b sin θ

    In this vertical direction, the student is not moving, because he transfers his momentum. The momentum transferred to the earth is equal to the vertical component of the book’s momentum in magnitude but opposite in direction. Thus;

    P_e = -P_ey

    P_e = – m_b•v_b•sinθ

    Thus, plugging in the relevant values to get ;

    P_e = -1.95 x 4.54 sin38

    P_e = -5.45 Kg.m/s

    The minus sign indicates that the direction of momentum is downwards

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )