Share
A pump, submerged at the bottom of a well that is 35 m deep, is used to pump water uphill to a house that is 50 m above the top of the well.
Question
A pump, submerged at the bottom of a well that is 35 m deep, is used to pump water uphill to a house that is 50 m above the top of the well. The density of water is 1,000 kg/m3. Neglect the effects of friction, turbulence, and viscosity. (a) Residents of the house use 0.35 m3 of water per day. The day’s pumping is completed in 2 hours during the day. i. Calculate the minimum work required to pump the water used per day ii. Calculate the minimum power rating of the pump. (b) In the well, the water flows at 0.50 m/s and the pipe has a diameter of 3.0 cm. At the house the diameter of the pipe is 1.25 cm. i. Calculate the flow velocity at the house when a faucet in the house is open. ii. Calculate the pressure at the well when the faucet in the house is open.
in progress
0
Physics
3 years
2021-08-10T09:43:40+00:00
2021-08-10T09:43:40+00:00 1 Answers
35 views
0

Answers ( )
Answer:
(a) i. The minimum work required to pump the water used per day is
291.85 kJ
ii. The minimum power rating of the pump is 40.53 Watts
(b) i. The flow velocity at the house when a faucet in the house is open where the diameter of the pipe is 1.25 cm is 2.87 m/s
ii. The pressure at the well when the faucet in the house is open is
837.843 kPa.
Explanation:
We note the variables of the question as follows;
Depth of well = 35 m deep
Height of house above the top of the well = 50 m
Density of water = 1000 kg/m³
Volume of water pumped per day = 0.35 m³
Duration of pumping of water per day = 2 hours
(a) i. We note that the energy required to pump the water is equivalent to the potential energy gained by the water at the house. That is
Energy to pump water = Potential Energy = m·g·h
Where:
m = Mass of the water
g = Acceleration due to gravity
h = Height of the house above the bottom of the well
Therefore,
Mass of the water = Density of the water × Volume of water pumped
= 1000 kg/m³ × 0.35 m³ = 350 kg
Therefore P.E. = 350 × 9.81 × (50 + 35) = 291847.5 J
Work done = Energy = 291847.5 J
Minimum work required to pump the water used per day = 291847.5 J
= 291.85 kJ
ii. Power is the rate at which work is done.
Power =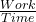
Since the time available to pump the water each day is 2 hours or 7200 seconds, therefore we have
Power = 291847.5 J/ 7200 s = 40.53 J/s or 40.53 Watts
(b)
i. If the velocity in the 3.0 cm pipe is 0.5 m/s
Then we have the flow-rate as Q = v₁ ×A₁
Where:
v₁ = Velocity of flow in the 3.0 cm pipe = 0.
A₁ = Cross sectional area of 3.0 cm pipe
As the flow rate will be constant for continuity, then the flow-rate at the faucet will also be equal to Q
That is Q = 0.5 m/s × π × (0.03 m)²/4 = 3.5 × 10⁻⁴ m³/s
Therefore the velocity at the faucet will be given by
Q = v₂ × A₂
∴ v₂ = Q/A₂
Where:
v₂ = velocity at the house the where the diameter of the pipe is 1.25 cm
A₂ = Cross sectional area of 1.25 cm pipe = 1.23 × 10⁻⁴ m²
Therefore v₂ = (3.5 × 10⁻⁴ m³/s)/(1.23 × 10⁻⁴ m²) = 2.87 m/s
ii. The pressure at the well is given by Bernoulli’s equation,
P₁ + 1/2·ρ·v₁² + ρ·g·h₁ = P₂ + 1/2·ρ·v₂² + ρ·g·h₂
If h₁ is taken as the reference point, then h₁ = 0 m
Also since P₂ is opened to the atmosphere, we take P₂ = 0
Therefore
P₁ + 1/2·ρ·v₁² + 0 = 0 + 1/2·ρ·v₂² + ρ·g·h₂
P₁ + 1/2·ρ·v₁² = 1/2·ρ·v₂² + ρ·g·h₂
P₁ = 1/2·ρ·v₂² + ρ·g·h₂ – 1/2·ρ·v₁²
= 1/2 × 1000 × 2.87² + 1000 × 9.81 × 85 – 1/2 × 1000 × 0.5²
= 837843.45 Pa = 837.843 kPa