A projectile is fired from a height of 80 M above sea level, horizontally with a speed of 360 M / S, calculate: The time it takes for the pr

Question

A projectile is fired from a height of 80 M above sea level, horizontally with a speed of 360 M / S, calculate: The time it takes for the projectile to reach the water. The Horizontal scope. The height that remains to descend after 2 seconds of being launched.

in progress 0
Edana Edana 4 years 2021-08-12T06:36:15+00:00 1 Answers 9 views 0

Answers ( )

  1. Helga
    0
    2021-08-12T06:37:50+00:00
    Reply

    Answer:

    (a) The projectile takes approximately 4.420 seconds to reach the water, (b) The horizontal scope of the projectile is 1591.2 meters, (c) The remaining height to descend after 2 seconds of being launched is 63.624 meters.

    Explanation:

    The projectile experiments a parabolic motion, where horizontal speed remains constant and accelerates vertically due to the gravity effect. Let consider that drag can be neglected, so that kinematic equation are described below:

    x = x_{o}+v_{o,x} \cdot t

    y = y_{o} + v_{o,y}\cdot t +\frac{1}{2}\cdot g \cdot t^{2}

    Where:

    x_{o}, y_{o} – Initial horizontal and vertical position of the projectile, measured in meters.

    v_{o,x}, v_{o,y} – Initial horizontal and vertical speed of the projectile, measured in meters per second.

    t – Time, measured in seconds.

    g – Gravitational acceleration, measured in meters per square second.

    x, y – Current horizontal and vertical position of the projectile, measured in meters.

    Given that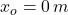 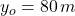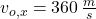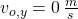x_{o} = 0\,m, y_{o} = 80\,m, v_{o,x} = 360\,\frac{m}{s}, v_{o,y} = 0\,\frac{m}{s} and g = -9.807\,\frac{m}{s^{2}}, the kinematic equations are, respectively:

    x = 360\cdot t

    y = 80-4.094\cdot t^{2}

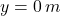    (a) If y = 0\,m, the time taken for the projectile to reach the water is:

    80 - 4.094\cdot t^{2} = 0

    t = \sqrt{\frac{80}{4.094} }\,s

    t \approx 4.420\,s

    The projectile takes approximately 4.420 seconds to reach the water.

    (b) The horizontal scope is the horizontal distance done by the projectile before reaching the water. If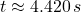 t \approx 4.420\,s, the horizontal scope of the projectile is:

    x = 360\cdot (4.420)

    x = 1591.2\,m

    The horizontal scope of the projectile is 1591.2 meters.

    (c) If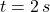 t = 2\,s, the height that remains to descend is:

    y = 80-4.094\cdot (2)^{2}

    y = 63.624\,m

    The remaining height to descend after 2 seconds of being launched is 63.624 meters.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )