A disk-shaped dough is initially spinning at 2 rotations per second (1 rotation = 360°). As time goes on, it slowly deforms, and is now spin

Question

A disk-shaped dough is initially spinning at 2 rotations per second (1 rotation = 360°). As time goes on, it slowly deforms, and is now spinning at a different angular speed. The dough changed radius from 16 cm to 17 cm, and its mass remained constant throughout. What is its final angular speed in degrees/s?

in progress 0
Doris 4 years 2021-08-11T11:20:34+00:00 1 Answers 16 views 0

Answers ( )

  1. thienthi
    0
    2021-08-11T11:22:21+00:00
    Reply

    Answer:

    10.44° per sec

    Explanation:

    Initial angular speed N = 2 rotations per minute

    converting to rad/s ω = 2πN/60 = (2 x 3.142 x 2)/60 = 0.21 rad/s

    the initial radius of the disk = 16 cm = 0.16 m

    final radius = 17 cm = 0.17 m

    Angular momentum = Iω

    where I = rotational inertia = mass x radius^{2}

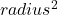
    ω = angular speed

    For the initial case

    I = m x 0.16^{2} = 0.0256m

    Angular momentum = 0.0256m x 0.21 = 0.0054m

    For second case

    I = m x 0.17^{2} = 0.0289m

    Angular momentum = 0.0289m x ω = 0.0289mω

    For conservation of rotational momentum, initial angular momentum must be equal to the final angular momentum

    0.0054m = 0.0289mω

    m cancels out, we have

    0.0054 = 0.0289ω

    ω = 0.187 rad/s

    converting back to rpm, we have

    N = 0.187/2π = 0.029 rotations per sec

    0.029 x 360 = 10.44° per sec

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )