A constant torque of 24.5 N · m is applied to a grindstone whose moment of inertia is 0.130 kg · m2. Using energy principles, and neglecting

Question

A constant torque of 24.5 N · m is applied to a grindstone whose moment of inertia is 0.130 kg · m2. Using energy principles, and neglecting friction, find the angular speed after the grindstone has made 16.9 revolutions. Hint: the angular equivalent of Wnet = FΔx = 1 2 mvf2 − 1 2 mvi2 is Wnet = τΔθ = 1 2 Iωf2 − 1 2 Iωi2. You should convince yourself that this last relationship is correct. (Assume the grindstone starts from rest.)

in progress 0
Trúc Chi 4 years 2021-07-29T21:23:24+00:00 1 Answers 473 views 1

Answers ( )

  1. Tryphena
    1
    2021-07-29T21:25:10+00:00
    Reply

    Answer:

    The final angular speed will be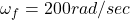 \omega _f=200rad/sec

    Explanation:

    We have given torque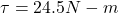 \tau =24.5N-m

    Moment of inertia is given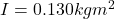 I=0.130kgm^2

    Angular speed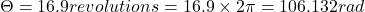 \Theta =16.9revolutions=16.9\times2\pi =106.132rad

    Initial angular velocity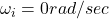 \omega _i=0rad/sec

    Work done is equal to

    w=\frac{1}{2}I\omega _f^2-\frac{1}{2}I\omega _i^2

    \tau (\Delta \Theta )=\frac{1}{2}I\omega _f^2

    24.5\times 106.132=\frac{1}{2}\times 0.130\times \omega _f^2

    \omega _f=200rad/sec

    So the final angular speed will be \omega _f=200rad/sec

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )