A block with mass 0.50 kg is forced against a horizontal spring of negligible mass, compressing the spring a distance of 0.20 m (Fig. P7.39)

Question

A block with mass 0.50 kg is forced against a horizontal spring of negligible mass, compressing the spring a distance of 0.20 m (Fig. P7.39). When released, the block moves on a horizontal tabletop for 1.00 m before coming to rest. The force constant k is 100 N>m. What is the coefficient of kinetic friction mk between the block and the tabletop?

in progress 0
Gerda 4 years 2021-09-02T01:01:48+00:00 2 Answers 43 views 0

Answers ( )

  1. Bo
    0
    2021-09-02T01:02:50+00:00
    Reply

    Answer:

    0.4

    Explanation:

    (i) Since the mass is forced against the spring, an elastic energy (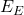E_{E}) due to the compression of the spring by the force is produced and is given according to Hooke’s law by;

    E_{E} = \frac{1}{2} k c²            ——————————–(i)

    Where;

    k = spring’s constant

    c = compression caused on the spring.

    From the question;

    k = 100N/m

    c = 0.20m

    Substitute these values into equation (i) as follows;

    E_{E} = \frac{1}{2} x 100 x 0.20²

    E_{E} = 2J

    (ii) Now, when the mass is released, it causes the block to move some distance until it stops thereby doing some work within that distance. This means that the elastic energy is converted to workdone. i.e

    E_{E} = W          ————(ii)

    The work done (W) is given by the product of the net force(F) on the block and the distance covered(s). i.e

    W = F x s           —————–(iii)

    But, the only force acting on the body as it moves is the frictional force (F_{R}) acting to oppose its motion. i.e

    F = F_{R}

    Where;

    F_{R} = μN      [μ = coefficient of kinetic friction, N = mg = normal reaction between the block and the tabletop, m = mass of the block, g = gravity]

    F_{R} = μ x mg

    Substitute F = F_{R} = μ x mg into equation (iii) as follows;

    W = μ x mg x s             —————-(iv)

    Now substitute the value of W into equation (ii) as follows;

    E_{E} = μ x mg x s                ——————(v)

    Where;

    E_{E} = 2 J               [as calculated above]

    m = 0.50 kg

    s = distance moved by block = 1.00m

    g = 10m/s²            [a known constant]

    Substitute these values into equation (v) as follows;

    2 = μ x 0.50 x 10 x 1

    2 = 5μ

    μ = 2 / 5

    μ = 0.4

    Therefore, the coefficient of kinetic friction between the block and the tabletop is 0.4

  2. thienthi
    0
    2021-09-02T01:02:50+00:00
    Reply

    Answer:

    μk = 0.408

    Explanation:

    Given:

    m=0.50 Kg,

    Let compressed distance x = 0.20 m, and

    stretched distance after releasing y = 1.00 m

    K = 100 N/M

    Sol:

    Law of conservation of energy

    Energy dissipation due to friction = P.E stores in the spring

    Ff * y = 1/2 K x ²   (Ff = μk Fn)  And (Fn = mg) so

    μk mgy  =   1/2 K x ²

    μk = 1/2 K x ² /mgy   Putting values

    μk = (1/2 ) (100 N/M) (0.20 m)² / (0.50 Kg x 9.8 m/s² x 1 m)

    μk = 0.408

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )