Share
A beach resort has 29 jet skis for guests to rent. Of these, 14 are two-person skis, 18 haveturbo packs, and 10 are both for two persons and
Question
A beach resort has 29 jet skis for guests to rent. Of these, 14 are two-person skis, 18 haveturbo packs, and 10 are both for two persons and have turbo packs. LetTbe the event that a jetski, randomly chosen, is a two-person ski, and letPbe the event that the ski has a turbo pack.A jet ski is chosen at random for rental. Find the probability for each of the following events.
in progress
0
Mathematics
4 years
2021-09-04T13:47:56+00:00
2021-09-04T13:47:56+00:00 1 Answers
11 views
0

Answers ( )
Questions:
a. The jet ski is for two persons and has turbo packs.
b. The jet ski is not for two persons but has turbo packs.
Answer:
Step-by-step explanation:
Given
Solving (a):
This is represented as: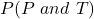
This is calculated as:
Solving (a):
This is represented as: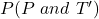
This is calculated as:
Using the complement rule, we have:
The equation becomes: