A 1000kg roller coaster begins at 10m tall hill with initial velocity of 6m/s and travels down until a second hill. 1700J is transformed to

Question

A 1000kg roller coaster begins at 10m tall hill with initial velocity of 6m/s and travels down until a second hill. 1700J is transformed to thermal engird by friction. In order for rollercoaster to get up 2nd hill it must have velocity of 4.6m/s or less at the top. What is the maximum height the second hill could be

in progress 0
Thái Dương 4 years 2021-08-11T05:38:35+00:00 1 Answers 207 views 0

Answers ( )

  1. hongcuc2
    0
    2021-08-11T05:40:11+00:00
    Reply

    Answer:

    The maximum height could be 10.6 meters.

    Explanation:

    For this kind of exercise, we use the general principle for conservation of mechanical energy (E) that states:

    E_1+W_f=E_2 (1)

    That means the mechanical energy an object has on a point 2 should be equal to the mechanical energy on a point 1 plus the energy transformed into heat due friction denoted as Wf (It is negative because is lost). In our case point 1 is the point where the roller coaster begins and point 2 is at the second hill. Tola mechanical energy is the sum of potential gravitational energy and kinetic energy, so (1) is :

    K_{1}+U_{1}+W_{f}=K_{2}+U_{2}

    with K the kinetic energy and U the potential energy, remember potential energy is mgh and kinetic energy is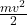 \frac{mv^2}{2} with m the mass, v the velocity and h the height, then:

    \frac{mv_1^2}{2}+mgh_1+W_{f}=\frac{mv_2^2}{2}+mgh_2

    Solving for h_2:

    h_2=\frac{\frac{mv_1^2}{2}+mgh_1+W_{f}-\frac{mv_2^2}{2}}{mg}=\frac{\frac{(1000)(6)^2}{2}+(1000)(9.8)(10)-1700-\frac{(1000)(4.6)^2}{2}}{(1000)(9.81)}

    h_2=10.6 m

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )