1. Suppose a teenager puts her bicycle on its back and starts the rear wheel spinning from rest to a final angular velocity of 250 rpm in 5.

Question

1. Suppose a teenager puts her bicycle on its back and starts the rear wheel spinning from rest to a final angular velocity of 250 rpm in 5.00 s. Radius of tire is 50 cm. What angle did the tire move through in those 5 secs

in progress 0
Thiên Ân 3 years 2021-08-23T08:01:15+00:00 1 Answers 24 views 0

Answers ( )

  1. trungdung22
    0
    2021-08-23T08:02:15+00:00
    Reply

    Answer:

    \theta=65.18rad

    Explanation:

    The angle in rotational motion is given by:

    \theta=\frac{w_o+w_f}{2}t

    Recall that the angular speed is larger than regular frequency (in rpm) by a factor of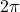 2\pi, so:

    \omega_f=2\pi f\\\omega_f=2\pi*250rpm\\\omega_f=1570.80 \frac{rad}{min}

    The wheel spins from rest, that means that its initial angular speed is zero(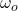\omega_o). Finally, we have to convert the given time to minutes and replace in the first equation:

    t=5s*\frac{1min}{60s}=0.083min\\\theta=\frac{\omega_f}{2}t\\\theta=\frac{1570.800\frac{rad}{min}}{2}(0.083min)\\\theta=65.18rad

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )