Light from a laser strikes a diffraction grating that has 5 308 grooves per centimeter. The central and first-order principal maxima are sep

Question

Light from a laser strikes a diffraction grating that has 5 308 grooves per centimeter. The central and first-order principal maxima are separated by 0.488 m on a wall 1.88 m from the grating. Determine the wavelength of the laser light. (In this problem, assume that the light is incident normally on the gratings.) nm

in progress 0
Thiên Thanh 4 years 2021-08-05T20:51:41+00:00 1 Answers 17 views 0

Answers ( )

  1. Helga
    0
    2021-08-05T20:53:23+00:00
    Reply

    Solution :

    Given :

    The angle of the first maximum with the center is given by :

    $a=\tan^{-1}\left(\frac{0.488}{1.88}\right)$

      = 14.5°

    The grating distance can be calculated as :

    $d=\frac{1 \ cm}{5308 \text{ slits}}$

       = $1.88 \times 10^{-4} \ m$

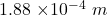
    When the principal maxima yields at y = 0.488 m and the length from the wall 1.88 m. Thus the equation of the wavelength is :

    $\lambda = g \times \frac{\sin a}{n}$  ,       where n = 1

      $=1.88 \times 10^{-4} \times \sin (14.5)$

     $=4.70 \times 10^{-5} \ m$

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )