Let V and W be vector spaces, and let T W V ! W be a linear transformation. Given a subspace U of V , let T .U / denote the set of all image

Question

Let V and W be vector spaces, and let T W V ! W be a linear transformation. Given a subspace U of V , let T .U / denote the set of all images of the form T .x/, where x is in U. Show that T .U / is a subspace of W .

in progress 0
Diễm Kiều 4 years 2021-08-23T02:31:54+00:00 1 Answers 145 views 0

Answers ( )

  1. ngocdiep
    0
    2021-08-23T02:33:46+00:00
    Reply

    Answer:

    #See solution for details:

    Explanation:

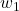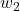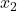    -If w_1 and w_2 are in T(U)  then there are x_1 and x_2 in U so that:

    T(x_)=-w_1\\\\T(x_)=w_2

    -Then :

    w_1+w_2=T(x_1)+T(x_2)=T(x_1+x_2)

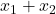    -But x_1+x_2 is in U since U is a subspace.

    -Also, for any scalar c we have:

    cw_1=cT(x_1)=T(cx_1), which is in T(U) since cx_1 is in U

    #Finally, 0=T(0) so 0 is in T(U) thus T(U) is a subspace of W as it satisfies the above 3 subspace conditions.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )