Share
Let surface S be the boundary of the solid object enclosed by x^2+z^2=4, x+y=6, x=0, y=0, and z=0. and, let f(x,y,z)=(3x)i+(x+y+2z)j + (3z)k
Question
Let surface S be the boundary of the solid object enclosed by x^2+z^2=4, x+y=6, x=0, y=0, and z=0. and, let f(x,y,z)=(3x)i+(x+y+2z)j + (3z)k be a vector field (for example, the velocityfaild of a fluid flow). the solid object has five sides, S1:bottom(xy-plane), S2:left side(xz-plane), S3 rear side(yz-plane), S4:right side, and S5:cylindrical roof.
a. Sketch the solid object.
b. Evaluate the flux of F through each side of the object (S1,S2,S3,S4,S5).
c. Find the total flux through surface S.
in progress
0
Physics
4 years
2021-08-11T06:18:17+00:00
2021-08-11T06:18:17+00:00 1 Answers
34 views
0

Answers ( )
a. I’ve attached a plot of the surface. Each face is parameterized by
•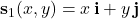 with
with 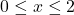 and
and 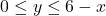 ;
;
•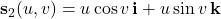 with
with 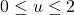 and
and 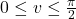 ;
;
•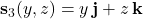 with
with 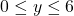 and
and 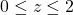 ;
;
•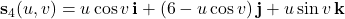 with
with 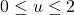 and
and 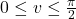 ; and
; and
•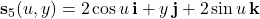 with
with 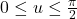 and
and 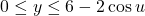 .
.
b. Assuming you want outward flux, first compute the outward-facing normal vectors for each face.
Then integrate the dot product of f with each normal vector over the corresponding face.
c. You can get the total flux by summing all the fluxes found in part b; you end up with 42π – 56/3.
Alternatively, since S is closed, we can find the total flux by applying the divergence theorem.
where R is the interior of S. We have
The integral is easily computed in cylindrical coordinates:
as expected.