integrate G(x,y,z)=yz over the surface of x+y+z=1 in the first octant.​

Question

integrate G(x,y,z)=yz over the surface of x+y+z=1 in the first octant.​

in progress 0
Hưng Khoa 3 years 2021-07-25T20:04:28+00:00 1 Answers 16 views 0

Answers ( )

  1. phucdien
    0
    2021-07-25T20:05:47+00:00
    Reply

    Parameterize the surface (I’ll call it S) by

    r(u, v) = (1 – u) (1 – v) i + u (1 – v) j + v k

    with 0 ≤ u ≤ 1 and 0 ≤ v ≤ 1.

    Take the normal vector to this surface to be

    n = ∂r/∂u × ∂r/∂v = ((v – 1) i + (1 – v) j) × ((u – 1) i – u j + k) = (1 – v) (i + j + k)

    with magnitude

    ||n|| = √3 (1 – v)

    Then in the integral, we have

    \displaystyle\iint_SG(x,y,z)\,\mathrm ds = \int_0^1\int_0^1 G((1-u)(1-v),u(1-v),v) \|\mathbf n\| \,\mathrm du\,\mathrm dv \\\\= \sqrt3 \int_0^1\int_0^1uv(1-v)^2\,\mathrm du\,\mathrm dv \\\\= \boxed{\frac1{8\sqrt3}}

    Alternatively, if you’re not familiar with parameterizing surfaces, you can use the “projection” formula:

    \displaystyle\iint_S G(x,y,z)\,\mathrm ds = \int_{S_{xy}}G(x,y,z)\sqrt{1+\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\,\mathrm dx\,\mathrm dy

    where I write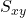 S_{xy} to mean the projection of the surface onto the (x, y)-plane, and z = f(x, y). We would then use

    x + y + z = 1   ==>   z = f(x, y) = 1 – x – y

    and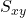 S_{xy} is the triangle,

    {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 – x}

    Then the integral becomes

    \displaystyle\int_0^1\int_0^{1-x}y(1-x-y)\sqrt{1+(-1)^2+(-1)^2}\,\mathrm dy\,\mathrm dx \\\\= \sqrt3\int_0^1\int_0^{1-x} y(1-x-y)\,\mathrm dy\,\mathrm dx \\\\= \frac{\sqrt3}{24} \\\\= \boxed{\frac1{8\sqrt3}}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )