In how many ways can we seat 3 pairs of siblings in a row of 7 chairs, so that nobody sits next to their sibling

Question

Question

in progress 0

Mathematics Thiên Hương 4 years 2021-08-05T09:36:27+00:00 2021-08-05T09:36:27+00:00 1 Answers 13 views 0

Answers ( )

Name*

E-Mail*

Website

Featured image

Browse

Captcha* Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )

Answer*

mocmien2 · Answer 1 · 2021-08-05T09:38:06+00:00

Answer:

1,968

Step-by-step explanation:

Let x₁ and x₂, y₁ and y₂, and z₁ and z₂ represent the 3 pairs of siblings, and let;

Set X represent the set where the siblings x₁ and x₂ sit together

Set Y represent the set where the siblings y₁ and y₂ sit together

Set Z represent the set where the siblings z₁ and z₂ sit together

We have;

Where the three siblings don’t sit together given as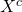 $X^c$ ∩ $Y^c$ ∩ $Z^c$

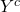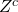
By set theory, we have;

Therefore;

Where;

$\left | U\right |$ = The number of ways the 3 pairs of siblings can sit on the 7 chairs = 7!

$\left | X\right |$ = The number of ways x₁ and x₂ can sit together on the 7 chairs = 2 × 6!

$\left | Y\right |$ = The number of ways y₁ and y₂ can sit together on the 7 chairs = 2 × 6!

$\left | Z\right |$ = The number of ways z₁ and z₂ can sit together on the 7 chairs = 2 × 6!

$\left | X \cap Y\right |$ = The number of ways x₁ and x₂ and y₁ and y₂ can sit together on the 7 chairs = 2 × 2 × 5!

$\left | X \cap Z\right |$ = The number of ways x₁ and x₂ and z₁ and z₂ can sit together on the 7 chairs = 2 × 2 × 5!

$\left | Y \cap Z\right |$ = The number of ways y₁ and y₂ and z₁ and z₂ can sit together on the 7 chairs = 2 × 2 × 5!

$\left | X \cap Y \cap Z\right |$ = The number of ways x₁ and x₂, y₁ and y₂ and z₁ and z₂ can sit together on the 7 chairs = 2 × 2 × 2 × 4!

Therefore, we get;

$\left | X^c \cap Y^c \cap Z^c \right |$ = 7! – (2×6! + 2×6! + 2×6! – 2 × 2 × 5! – 2 × 2 × 5! – 2 × 2 × 5! + 2 × 2 × 2 × 4!)

$\left | X^c \cap Y^c \cap Z^c \right |$ = 5,040 – 3072 = 1,968

The number of ways where the three siblings don’t sit together given as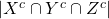 $\left | X^c \cap Y^c \cap Z^c \right |$ = 1,968