In a Young’s double-slit experiment, a set of parallel slits with a separation of 0.102 mm is illuminated by light having a wavelength of 57

Question

In a Young’s double-slit experiment, a set of parallel slits with a separation of 0.102 mm is illuminated by light having a wavelength of 575 nm and the interference pattern observed on a screen 3.50 m from the slits.(a) What is the difference in path lengths from the two slits to the location of a second order bright fringe on the screen?(b) What is the difference in path lengths from the two slits to the location of the second dark fringe on the screen, away from the center of the pattern?

in progress 0
Sapo 4 years 2021-08-11T05:34:01+00:00 1 Answers 11 views 0

Answers ( )

  1. quangkhai
    0
    2021-08-11T05:36:00+00:00
    Reply

    Answer:

    Rounded to three significant figures:

    (a)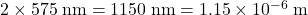 2 \times 575\; \rm nm = 1150\; \rm nm = 1.15\times 10^{-6}\; \rm m.

    (b)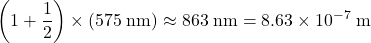 \displaystyle \left(1 + \frac{1}{2}\right) \times (575\;\rm nm) \approx 863\; \rm nm = 8.63\times 10^{-7}\; \rm m.

    Explanation:

    Consider a double-slit experiment where a wide beam of monochromatic light arrives at a filter with a double slit. On the other side of the filter, the two slits will appear like two point light sources that are in phase with each other. For each point on the screen, “path” refers to the length of the segment joining that point and each of the two slits. “Path difference” will thus refer to the difference between these two lengths.  

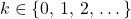    Let k denote a natural number (k \in \left\lbrace0,\, 1,\, 2,\, \dots\right\rbrace.) In a double-split experiment of a monochromatic light:

    • A maximum (a bright fringe) is produced when light from the two slits arrive while they were in-phase. That happens when the path difference is an integer multiple of wavelength. That is: \text{Path difference} = k\, \lambda.
    • Similarly, a minimum (a dark fringe) is produced when light from the two slits arrive out of phase by exactly one-half of the cycle. For example, The first wave would be at peak while the second would be at a crest when they arrive at the screen. That happens when the path difference is an integer multiple of wavelength plus one-half of the wavelength: \displaystyle \text{Path difference} = \left(k + \frac{1}{2}\right)\cdot \lambda.

    Maxima

    The path difference is at a minimum (zero) at the center of the screen between the two slits. That’s the position of the first maximum- the central maximum, a bright fringe where k = 0 in \text{Path difference} = 0.

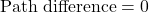    The path difference increases while moving on the screen away from the center. The first order maximum is at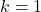 k = 1 where \text{Path difference} = \lambda.

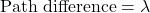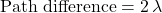    Similarly, the second order maximum is at k = 2 where \text{Path difference} = 2\, \lambda. For the light in this question, at the second order maximum: \text{Path difference} = 2\, \lambda = 2 \times 575\; \rm nm = 1.15\times 10^{-6}\; \rm m.

    • Central maximum: k = 0, such that \text{Path difference} = 0.
    • First maximum: k = 1, such that \text{Path difference} = \lambda.
    • Second maximum: k = 2, such that \text{Path difference} = 2\, \lambda.

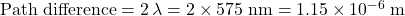    Minima

    The dark fringe closest to the center of the screen is the first minimum.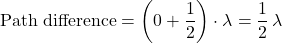 \displaystyle \text{Path difference} = \left(0 + \frac{1}{2}\right)\cdot \lambda = \frac{1}{2}\, \lambda at that point.

    Add one wavelength to that path difference gives another dark fringe- the second minimum.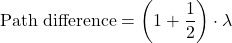 \displaystyle \text{Path difference} = \left(1 + \frac{1}{2}\right)\cdot \lambda at that point.

    • First minimum: k =0, such that \displaystyle \text{Path difference} = \frac{1}{2}\, \lambda.
    • Second minimum: k =1, such that \displaystyle \text{Path difference} = \left(1 + \frac{1}{2}\right)\cdot \lambda.

    For the light in this question, at the second order minimum: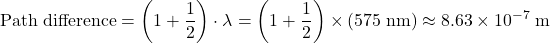 \displaystyle \text{Path difference} = \left(1 + \frac{1}{2}\right)\cdot \lambda = \left(1 + \frac{1}{2}\right)\times (575\; \rm nm) \approx 8.63\times 10^{-7}\; \rm m.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )