If the specific surface energy for magnesium oxide is 1.0 J/m2 and its modulus of elasticity is (225 GPa), compute the critical stress requi

Question

If the specific surface energy for magnesium oxide is 1.0 J/m2 and its modulus of elasticity is (225 GPa), compute the critical stress required for the propagation of an internal crack of length 0.3 mm.

in progress 0
Xavia 4 years 2021-08-19T09:20:34+00:00 1 Answers 5 views 0

Answers ( )

  1. Doris
    0
    2021-08-19T09:22:25+00:00
    Reply

    Answer:

    The critical stress required for the propagation of an initial crack              \sigma_{c} =  21.84 M pa

    Explanation:

    Given data

    Modulus of elasticity E = 225 × 10^{9} \frac{N}{m^{2} }

    Specific surface energy for magnesium oxide is \gamma_{s} = 1 \frac{J}{m^{2} }

    Crack length (a) = 0.3 mm = 0.0003 m

    Critical stress is given by 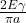\sigma_{c}^{2} } = \frac{2 E \gamma}{\pi a} ——– (1)

    ⇒ 2 E \gamma_{s} = 2 × 225 × 10^{9} × 1 = 450 × 10^{9}

    ⇒ \pi a = 3.14 × 0.0003 = 0.000942  

    ⇒ Put these values in equation 1 we get

    ⇒ \sigma_{c}^{2} } = \frac{450 }{0.000942} 10^{9}

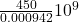
    ⇒ \sigma_{c}^{2} } = 4.77 × 10^{14}

    ⇒ \sigma_{c} = 2.184 × 10^{7} \frac{N}{m^{2} }

    ⇒ \sigma_{c} =  21.84 \frac{N}{mm^{2} }

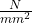
    ⇒ \sigma_{c} =  21.84 M pa

    This is the critical stress required for the propagation of an initial crack.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )